Dijkstra最短路算法讲解
你说得对,但是迪克斯特拉算法(Dijkstra)是由荷兰计算机科学家狄克斯特拉于1959年提出的,因此又叫狄克斯特拉算法。是从一个顶点到其余各顶点的最短路径算法,解决的是有权图中最短路径问题。迪杰斯特拉算法主要特点是从起始点开始,采用贪心算法的策略,每次遍历到始点距离最近且未访问过的顶点的邻接节点,直到扩展到终点为止。
很简单就能理解,举个例子,我们就以下图的多节点、多路径图来讲解一下Dijkstra算法寻找最短路径的过程。(这个图可能有点看不清, B-E 的距离是 6 , C-D 的距离是 15 ,这个图这俩数……qwq)
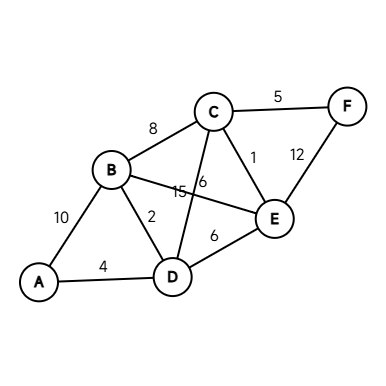
你看,从 A 开始,直接能到的点有 B E 。之后我们将除此之外的其他点到 A 的距离视为无穷大( 0x3F3F3F3F3F3F3F3F ),之后我们将每个点到自身的距离视为 0 。
那么,在最开始的时候, A 到诸点的距离如下。
| A | B | C | D | E | F |
|---|---|---|---|---|---|
| 0 | 10 ( A-B ) | 无穷大 | 4 ( A-D ) | 无穷大 | 无穷大 |
OK!接下来,我们找一个除了 A ,到 A 距离最短的点。很明显,是 D 对不对。
所以,目前最优的路径就是 A-D ,我们以 A-D 的距离更新其他的点,可以得出:
| A | B | C | D | E | F |
|---|---|---|---|---|---|
| 0 | 6 ( A-D-B ) | 19 ( A-D-C ) | 4 | 10 ( A-D-E ) | 无穷大 |
把俩表的 A 到各点的距离取最小值,得出:
| A | B | C | D | E | F |
|---|---|---|---|---|---|
| 0 | 6 ( A-D-B ) | 19 | 4 | 10 | 无穷大 |
之后我们不看 A 和 D (这俩点已经操作完了),可以看出当前最有的路径是 A-D-B ,我们就以 A-D-B 的距离更新其他的点,可得:
| A | B | C | D | E | F |
|---|---|---|---|---|---|
| 0 | 6 | 14 ( A-D-B-C ) | 4 | 12 ( A-D-E ) | 无穷大 |
还是和以前的取最小值:
| A | B | C | D | E | F |
|---|---|---|---|---|---|
| 0 | 6 | 14 | 4 | 10 | 无穷大 |
我们只需要重复这步骤,最终的结果就是:
| A | B | C | D | E | F |
|---|---|---|---|---|---|
| 0 ( A-A ) | 6 ( A-D-B ) | 11 ( A-D-E-C ) | 4 ( A-D ) | 10 ( A-D-E ) | 16 ( A-D-E-C-F ) |
